Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 암호화
- 반도체 엔지니어
- 던전앤파이터
- 면접
- 유니티에러
- 반도체
- 네트워크
- 던파
- 네오플
- 머신러닝
- 반도체 취업
- 아두이노
- 에러
- 이더리움
- MuchineRunning
- memory
- 아두이노함수
- 메모리
- 컴퓨터구조
- MLAgent
- 레지스터
- neople
- 게임기획
- 보안
- 인터럽트
- 아두이노우노
- Unity
- 네트워크보안
- 메타마스크
- 유니티
Archives
- Today
- Total
Dreaming Deve1oper
부동 소수점 (BFPN) 본문
BFPN : 단 정밀도 (Single Precision)
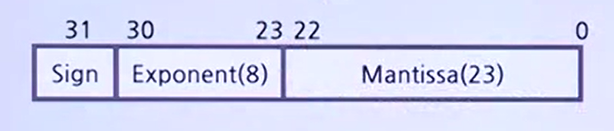
- 기본형 ±0.1M*2^E
- 1.1010*2^4 -> 0.1101*2^5 로 정규화.
- S= 0
- E= 0000_0101 (2's Complement 표현)
- M= 101_0000_0000_0000_0000_0000 (Unsigned 표현)
- S와 M을 합쳐서 Signed Magnitude로 표현.
BFPN: 배 정밀도 (Double Precision)

- Sign = 1 (음수), 0 (양수)
- Mantissa(가수)의 범위: 0.5≤Mantissa≤1 -> 정밀도 결정
- Exponent 범위: -2^7<Exponent<2^7-1 -> 표현 가능한 수의 범위 결정
- Mantissa와 Exponent간 길이 조정이 필요
단 정밀도 BFPN의 표현가능 범위


단 정밀도 & biased exponent
Bias=128일 경우 N= 13.625에 대한 BFPN 표현

- S= 1
- M= 10110100000000000000000 (소수점 우측의 첫 번째 1 제외)
- E= 00000100 + 10000000 = 10000100 (Bias 128을 더함)

Why Biased Exponent?
- E의 값이 아주 작은 음수라면 전체 숫자는 거의 0에 가까워짐.
- 0에 대한 표현에서 모든 Bit들이 0이 되게 하여 Zero-Test(ZT)가 정수에서와 같은 방법으로 가능하게 하기 위함.
- IF M = 000_0000_0000_0000_0000_0000 then BFPN=0 | 일반적인 정수와 동일한 방법으로 ZT 가능.
- IF E = 1000_0000 (BFPN에서 가장 작은 음수) then BFPN=0 | 일반적인 정수와 동일한 방법으로 ZT 불가능.
- IF E = 0000_0000 (BFPN with Baised 128에서 가장 작은 음수) then BFPN=0 | 일반적인 정수와 동일한 방법으로 ZT 가능.
| Exponent 패턴 | 절대값 | 실제 Exponent 값 | |
| Bias= 127 | Bias= 128 | ||
| 11111111 | 255 | +128 | +127 |
| 11111110 | 254 | +127 | +126 |
| ... | ... | ... | ... |
| 10000001 | 129 | +2 | +1 |
| 10000000 | 128 | +1 | 0 |
| 01111111 | 127 | 0 | -1 |
| 01111110 | 126 | -1 | -2 |
| ... | ... | ... | ... |
| 00000001 | 1 | -126 | -127 |
| 00000000 | 0 | -127 | -128 |


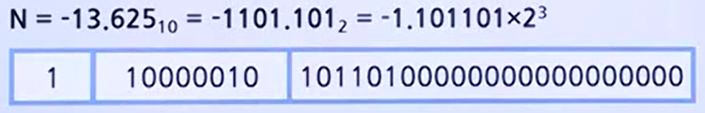
'컴퓨터 구조' 카테고리의 다른 글
| CPU의 구조와 구성 요소 (0) | 2022.03.26 |
|---|---|
| ALU: Arithmetic Operations (0) | 2022.03.20 |
| Integer Arithmetic / 정수 산술 연산 (Day 2) (0) | 2022.03.19 |
| 로직 연산 (Day 2) (0) | 2022.03.19 |
| ALU 아키텍처 / Integer 표현 (Day 2) (0) | 2022.03.19 |
Comments




