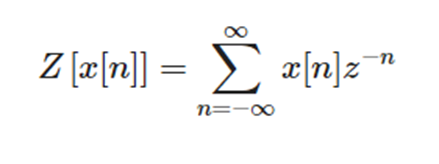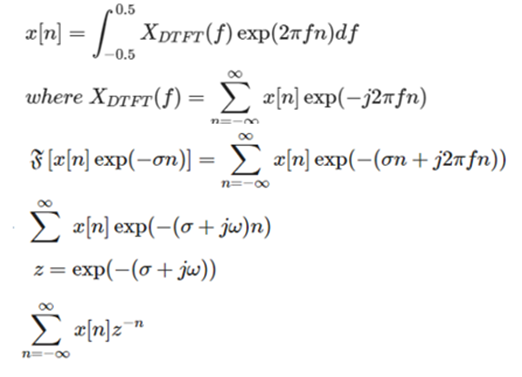| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 네오플
- 컴퓨터구조
- MLAgent
- 암호화
- Unity
- 면접
- 인터럽트
- 에러
- 반도체
- 아두이노
- MuchineRunning
- 아두이노함수
- 반도체 취업
- 이더리움
- 유니티에러
- 반도체 엔지니어
- 네트워크
- 메모리
- neople
- 메타마스크
- 네트워크보안
- 게임기획
- 던파
- 던전앤파이터
- 유니티
- 아두이노우노
- 머신러닝
- memory
- 레지스터
- 보안
- Today
- Total
Dreaming Deve1oper
z 변환의 용도 2 본문
z변환의 용도 추가 포스팅
하단의 링크는 필자가 작성했던 z변환의 용도에 관한 포스팅입니다.
z 변환의 용도 6가지
z 변환의 용도 이번 포스팅에선 z 변환의 용도 6가지와 그에 대해 포스팅해보고자 한다. 1. 필터의 안정도 판별 어떤 시스템의 안정도를 판별하는데 사용한다. 극점이 단위원 안에 있으면 안정으
juhuyunjjung.tistory.com
1. 극점과 영점
Pole(극점)과 zero(영점)의 위치는 시스템 특성에 영향을 미친다.
전달함수는 임펄스 응답의 z변환 형태이므로 전달함수 값을 알고 있다는 것은 시스템 특성을 알고 있다는 뜻이다.
다시말해 시스템을 해석할 수 있다는 의미이며 이는 전달함수의 극점, 영점이 시스템의 특성을 결정한다는 것이다.
시스템 설계적인 측면에서 극점을 0이라고 가정하면, 이는 모든 주파수에서 중심이므로 영향력이 없게 된다.
즉, 0에 존재하는 극점 그리고 영점은 시스템에 영향을 미치지 못한다는 의미이다.
극점의 위치가 z=0.9 인 경우 극점은 분모가 무한대가 되기 때문에 H(z)가 발산한다는 의미이다.
따라서 극점의 근처에서는 H(z) 값이 매우 커지며 멀어질수록 값이 점점 작아질 것이다. 극점의 위치(0.9)는 Low frequency와 가까우므로 Low frequency 에서 출력 증폭 비율이 높고 High frequency 에서는 낮을 것이다.
즉, 위의 특성을 갖는 시스템은 LPF (Low Pass Filter)이다.
2. 이산 시스템의 해석
라플라스 변환이 연속 시간 시스템에 이용되는 것과 마찬가지로 z 변환은 이산 시스템의 해석에 사용될 수 있다.
z=exp(jω)를 z 변환에서 이산 시간 전달함수에서 대입하면 시스템 주파수 응답을 확인할 수 있다.
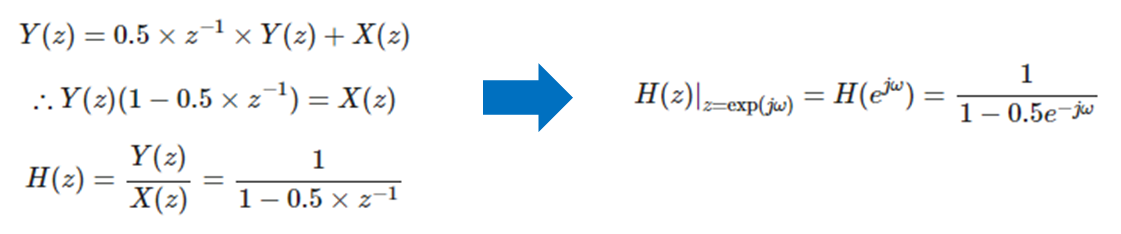
y[n]=0.5y[n-1]+x[n]이라는 AR 시스템에 대하여 z 변환을 해주면 다음과 같은 수식을 얻을 수 있다.
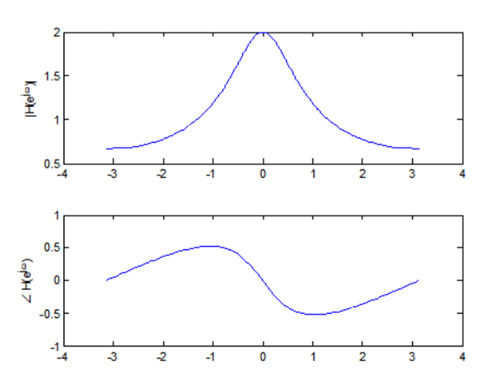
이 경우에 주파수 응답을 얻기 위해 z=exp(jω)를 대입하면 다음과 같은 결과를 얻을 수 있다.위의 수식들을 도시하면 그림과 같음을 확인할 수 있다.
이는 LPF (Law Pass Filter)의 성질을 갖는 시스템임을 알 수 있다.
3. 차분방정식
이산신호 x[n]에 대해 위와 같은 변환을 z변환이라고 한다.
Z변환은 좁은 의미에서는 선형 차분 방정식(Linear Difference Equation)을 쉽게 풀 수 있도록 도와준다.좀 더 넓은 의미에서는 DTFT (Discrete Time Fourier Transform)의 일반화된 형태라고 이해할 수 있다.
이것은 컨볼루션 계산에서의 CTFT와 라플라스 변환의 관계와 비유되는 것이 가장 알맞다.DTFT는 z 변환의 특수한 경우라고 말할 수 있으며 DTFT의 일반적인 형태라는 의미이다.DTFT의 수식으로부터 z 변환의 수식을 유도하면 수학적으로 DTFT와 z 변환이 닮았음을 확인할 수 있다.
이 유도 방식은 z 변환과 DTFT의 관계에 대해 보여준다.
이 과정을 통해 z 변환과 DTFT가 라플라스 변환 그리고 CTFT의 관계와 얼마나 닮았는지 확인해 볼 수 있다. DTFT는 z 변환의 특수한 경우인데 그것은 원의 반지름이 1인 경우에 z 변환을 취한 것과 같은 경우이다.
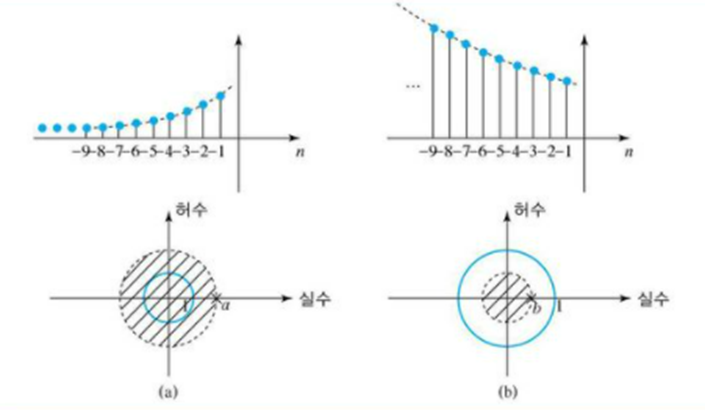
4. 안정도 판별두개의 결과로부터 임펄스 응답이 우측신호인 경우
-> 극점이 단위원 내에 있을 경우 이는 안정 시스템이다.
-> 수렴영역이 단위원을 포함하는 경우 안정시스템이다.
두개의 결과로부터 임펄스 응답이 좌측신호인 경우
-> 수렴영역이 단위원을 포함하는 경우 안정시스템이다.
-> 수렴영역이 단위원을 포함하는 경우 안정 시스템이다.
임펄스 응답이 우측신호인 경우와 좌측 시스템인 경우 수렴영역이 단위원을포함하면, 이는 안정시스템임을 의미한다.
단, 극점으로 안정도를 판별하는 경우엔 주의가 필요하다.
임펄스 응답이 우측신호 (주로 인과 시스템)인 경우에는 극점이 단위원 안에 존재하면 이는 안정 시스템이기 때문이다.
5. IIR 필터의 z 변환IIR 필터는 현재의 출력을 계산하는데 입력신호 뿐만 아니라, 이미 출력된 신호가 다시 이용된다.
FIR 시스템은 유한한 개수의 입력에 유한한 개수의 출력이 나오므로 항상 안정하지만
IIR 시스템은 출력이 다시 입력으로 들어오고 시스템이 발산해버리는 경우가 있을 수 있다.
안정하지 않은 시스템에 대한 해석은 의미가 없다는 것이다.결론적으로 극점의 절대값이 단위원보다 크면, 시스템은 불안정하다.
극점이 단위원 내에 존재하므로 이 IIR 시스템은 안정한 시스템임을 의미한다. 또한 n domain의 임펄스 응답이 수렴하므로 안정하다는 것을 알 수있다.
주파수 응답 곡선을 피해 z domain의 영점에 해당하는 주파수의 신호는 저지하며 극점 부분에 해당하는 주파수의 신호는 통과시키는 BPF 특성을 갖는다.
'DSP' 카테고리의 다른 글
| z 변환의 용도 6가지 (0) | 2022.02.18 |
|---|---|
| z 변환이란? (0) | 2022.02.18 |
| z 변환의 용도 (0) | 2021.12.17 |